Ant colony system. Combinatorial optimization
Combinatorial optimization problems are virtually impossible to brute-force. Whether finding the minimal distance through all cities, scheduling jobs on machines or packing a knapsack, there is no straight-forward approach. These problems are NP-hard. To solve some of them one may use ant colony optimization, a stochastic technique inspired by the behavior of ants, i.e. pheromone secretion on common paths. This project utilizes an ant colony system constrained to given points on a plane, in order to find the shortest path that visits all of them exactly once.
Visit the project repository here!
The problem is to determine the shortest path going through every city given by coordinates, like this:
x = [3 2 12 7 9 3 16 11 9 2]; y = [1 4 2 4.5 9 1.5 11 8 10 7];
x = [3 2 12 7 9 3 16 11 9 2]; y = [1 4 2 4.5 9 1.5 11 8 10 7];
First, the distances are calculated and equal trace of pheromone is placed on every path between the cities. Then, ants_count ants are created, with a boolean vector of visited cities and two variables, storing tour length and current city (visible below). Each ant is also assigned a value in a dictionary tours, corresponding to the cities it traveled to on its tour, in order. A random selection of starting points is performed for our ants, which will remain their starting points throughout the algorithm, hence the name hometowns.
Each ant then chooses the next city to go to, based on the amount of pheromone on feasible paths and the distance. Probability of choosing city j is given by the j-th column in the decision table a, where indices represent ants. When each ant visits all N cities, the pheromones of the best ants are deposited on appropriate paths and our cybernetic insects start the tour again, until they perform set amount of tours.
After each iteration, the shortest path is evaluated, and the optimal path is selected from all the tours. The results are presented on a graph, representing the map of considered cities, with gray connections being the amount of pheromones squared, and the green line being the optimal path (figures below). A preview of the shortest path in each tour is available, together with the percentage of the ants that took it. The optimal path and its length are then printed out. For ants_count = 20 the optimal solution is more frequent towards the final tours and the less ants are allowed to leave the pheromone, the higher likelihood of getting stuck on a suboptimal path.
"""
Implementation of Ant Colony System for the travelling salesman problem.
We are given a map containing 10 cities on 2d plane. In order to find the
shortest path that goes through all of them we utilize simulated ants,
depositing pheromones in greater amount on shorter paths and then choosing
the paths with more pheromone on them. The ants also have a memory of the
visited cities, otherwise it's just a stochastic process.
"""
import math
import random as rnd
import pandas as pd
import matplotlib.pyplot as plt
class AntColonySystem:
"""Class handling ants and map creation, iterations and more."""
def __init__(self, ants_count, alpha=1, beta=5, rho=0.5, tau_0=0.1):
"""
Create a simulation object by specifying needed parameters.
m - the number of ants
alpha, beta - decision coefficients (pheromone and distance)
rho - pheromone evaporation coefficient
tau_0 - initial pheromone amount
"""
self.ants_count = ants_count
self.alpha = alpha
self.beta = beta
self.rho = rho
self.tau_0 = tau_0
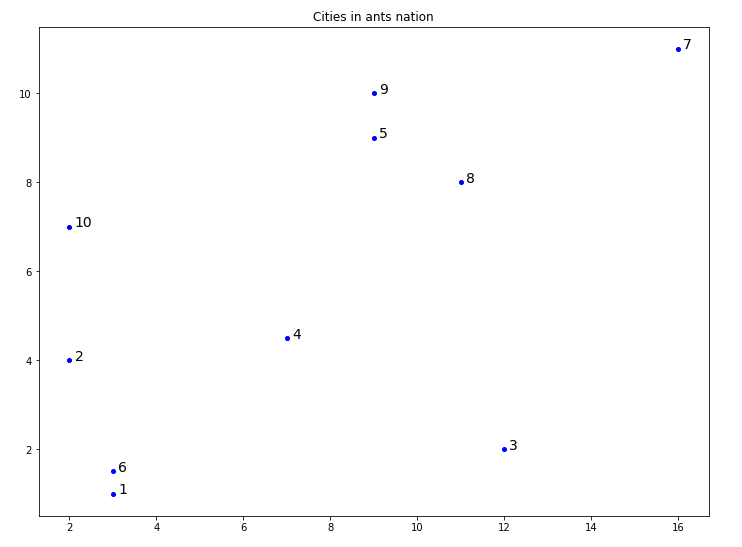
def open_map(self, map_id):
"""Use the provided data file to import the coordinates of cities."""
self.map_id = map_id
cities = open(f'data/AS_map_{map_id}.txt')
for line in cities:
line = line.strip()
if line[0] == 'x':
self.x = list(map(float, line[5:-2].split()))
if line[0] == 'y':
self.y = list(map(float, line[5:-2].split()))
# Check validity of coordinates in the file
if len(self.x) != len(self.y):
raise SystemExit("Cities coordinates invalid")
self.N = len(self.x)
return self.N
def prepare_distance_table(self):
"""Calculate the euclidean distance between each two cities."""
self.d = pd.DataFrame(data=self.tau_0, index=range(1, self.N+1),
columns=range(1, self.N+1))
for city_1 in self.d:
self.d[city_1] = [self.distance(city_1, city_2)
for city_2 in self.d.index]
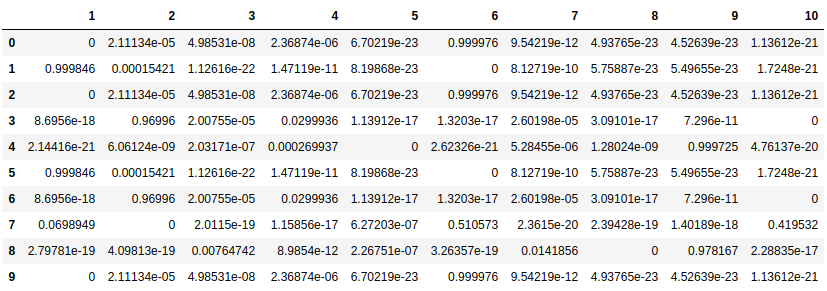
def prepare_pheromone_table(self):
"""Calculate the amount of pheromone between each two cities."""
self.tau = pd.DataFrame(data=self.tau_0, index=range(1, self.N+1),
columns=range(1, self.N+1))
for i in self.tau.index:
self.tau.loc[i, i] = 0
def set_hometowns(self):
"""Create a list of fixed starting points for each ant."""
self.hometowns = [rnd.randint(1, self.N)
for _ in range(ant_colony.ants_count)]
def spawn_ants(self):
"""Create a table of ants, with a record of visited cities."""
self.ants = pd.DataFrame(data=False, index=range(self.ants_count),
columns=range(1, self.N+1))
self.ants['Current'] = self.hometowns
self.ants['TourLength'] = 0.0
for ant in self.ants.index:
self.ants.loc[ant, self.ants.loc[ant, 'Current']] = True
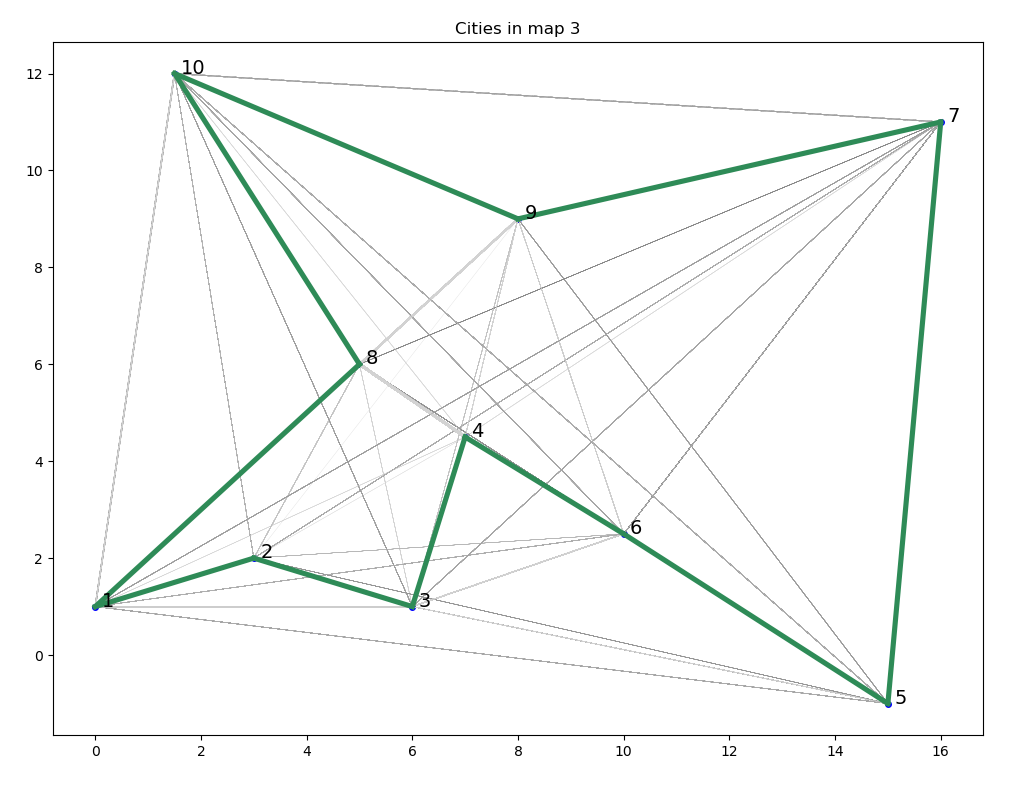
def draw_map(self):
"""Draw a map of the cities."""
self.fig, self.ax = plt.subplots()
self.fig.set_size_inches(12, 9)
self.ax.plot(self.x, self.y, 'bo', ms=4)
self.ax.set_title(f'Cities in map {self.map_id}')
for i in range(0, self.N):
self.ax.annotate(i+1, (self.x[i]+0.12, self.y[i]), fontsize=14)
def ants_tour_complete(self):
"""Return whether all ants visited all the cities."""
return (self.ants.xs(range(1, self.N+1), axis=1).all()).all()
def calculate_decision_table(self):
"""Calculate a decision table with probability of taking each path."""
# Probability proportional to pheromone amount over distance
a_naive = (self.tau**self.alpha/self.d**self.beta).fillna(0)
# Dividing probabilities by the sum of eligible neighbours
self.a = pd.DataFrame(index=self.ants.index, columns=a_naive.columns)
for ant in self.ants.index:
current = self.ants.loc[ant, 'Current']
neighbourhood = sum(a_naive[current]
* ~self.ants.loc[ant][:self.N])
self.a.loc[ant] = ((a_naive[current] / neighbourhood)
* ~self.ants.loc[ant][:self.N])
def choose_next_cities(self):
"""Return a series of next moves for each ant."""
next_cities = pd.Series(index=self.ants.index, data=0)
for ant in self.a.index:
preferred = pd.to_numeric(self.a.loc[ant]).fillna(0)
its_my_goddamn_choice = rnd.random()
while(len(preferred) > 0):
best_city = preferred.idxmax()
if (its_my_goddamn_choice <= preferred[best_city]):
next_cities.loc[ant] = best_city
break
else:
its_my_goddamn_choice -= preferred[best_city]
preferred.drop(best_city, inplace=True)
return next_cities
def finish_in_hometowns(self):
"""Add a final path to the tour, from current city to hometown."""
for ant in self.ants.index:
current = self.ants.loc[ant, 'Current']
self.ants.loc[ant, 'TourLength'] += self.distance(
current, self.hometowns[ant])
self.draw_path(current, self.hometowns[ant], 'grey',
self.tau.at[current, self.hometowns[ant]])
self.ants.loc[ant, 'Current'] = self.hometowns[ant]
def update_pheromones(self, tours, elite_ants_count=4):
"""Evaporate some of the existing pheromones and deposit new."""
# Evaporte some of the pheromone
self.tau *= (1 - self.rho)
# Store best N ants in a dictionary with their tour lengths
elite_ants = {ant: self.ants.loc[ant, 'TourLength'] for ant in tours}
elite_ants = dict(sorted(elite_ants.items(), key=lambda ant: ant[1]))
elite_ants = list(elite_ants.items())[:elite_ants_count]
# Add pheronome only on the elite ants paths
for ant, best_length in elite_ants:
for city in range(self.N):
self.tau.at[tours[ant][city], tours[ant][(city+1) % self.N]] \
+= 1/best_length
self.tau.at[tours[ant][(city+1) % self.N], tours[ant][city]] \
+= 1/best_length
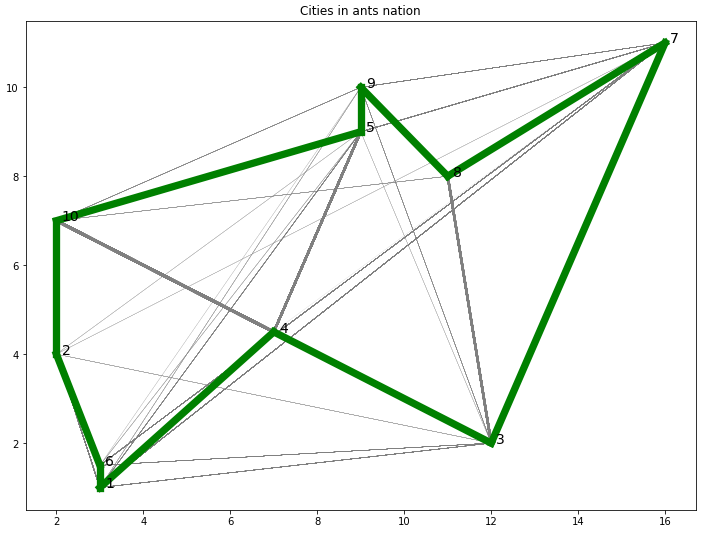
def draw_shortest_path(self, shortest_path):
"""Draw in green the shortest path from all iterations."""
for city in range(self.N):
self.draw_path(shortest_path[city],
shortest_path[(city+1) % self.N],
'seagreen', 0.6)
def distance(self, city_1, city_2):
"""Calculate distance between two cities based on their id numbers."""
x_1 = self.x[city_1 - 1]
x_2 = self.x[city_2 - 1]
y_1 = self.y[city_1 - 1]
y_2 = self.y[city_2 - 1]
return math.sqrt(pow(x_1 - x_2, 2) + pow(y_1 - y_2, 2))
def draw_path(self, city_1, city_2, line_color, pheromone):
"""Draw a line between cities, thickness based on pheromone amount."""
x_1 = self.x[city_1 - 1]
x_2 = self.x[city_2 - 1]
y_1 = self.y[city_1 - 1]
y_2 = self.y[city_2 - 1]
self.ax.plot([x_1, x_2], [y_1, y_2],
color=line_color, linewidth=(10*pheromone**2+0.1))
if __name__ == "__main__":
# Create an ant colony and prepare the environment
ant_colony = AntColonySystem(20, alpha=0.5)
ant_colony.open_map(3)
ant_colony.prepare_distance_table()
ant_colony.prepare_pheromone_table()
ant_colony.set_hometowns()
ant_colony.draw_map()
# Number of iterations (repeated tour taking)
TOTAL_ITERATIONS = 50
# Set the shortest path length holder variable
shortest_path_length = sum(ant_colony.d.unstack())
# Drop all ants on the map for the given number of times
for iteration in range(TOTAL_ITERATIONS):
# Create an internal table of ants with memory of visited citites
ant_colony.spawn_ants()
# Set up a dictionary of cities visited by each ant in order
tours = {ant: [ant_colony.ants.loc[ant, 'Current']]
for ant in ant_colony.ants.index}
# Until there is at least one unvisited city by at least by one ant
while (~ant_colony.ants_tour_complete()):
# Prepare a decision table with probabilities of chosing cities
ant_colony.calculate_decision_table()
# Selecting next cities to travel to
next_cities = ant_colony.choose_next_cities()
# Travelling to the chosen city
for ant in ant_colony.ants.index:
current = ant_colony.ants.loc[ant, 'Current']
# Calculate distanace, add to tour length
ant_colony.ants.loc[ant, 'TourLength'] \
+= ant_colony.distance(current, next_cities[ant])
# Plot the travel from current city to the next one on a map
ant_colony.draw_path(current, next_cities[ant], 'lightgrey',
ant_colony.tau.at[current,
next_cities[ant]])
# Set new city as the current city, add to tour
ant_colony.ants.loc[ant, 'Current'] = next_cities[ant]
tours[ant].append(next_cities[ant])
# Update visited cities
ant_colony.ants.loc[ant,
ant_colony.ants.loc[ant, 'Current']] = True
# After the complete tour go back to respective hometowns
ant_colony.finish_in_hometowns()
# Evaporate some and deposit new pheromones
ant_colony.update_pheromones(tours, elite_ants_count=6)
# Evaluate shortest travel distance
for ant in tours:
if ant_colony.ants.loc[ant, 'TourLength'] <= \
shortest_path_length:
shortest_path_length = ant_colony.ants.loc[ant, 'TourLength']
shortest_path = tours[ant]
# Print the shortest distance in this iteration
iter_best = min(ant_colony.ants['TourLength'])
print(f'Shortest path length in iteration {iteration+1}: {iter_best}')
# Draw the shortest path on the map
ant_colony.draw_shortest_path(shortest_path)
# Output the final result
print(f'Shortest path: {shortest_path}\nLength: {shortest_path_length}\n')
plt.show()